
Most of us learned in school how to do matrix multiplication, and then most of us probably promptly forgot it. It is a topic that is neither challenging nor interesting, but it will give us a good starting point for my foray into ParallelFX. If you need a quick refresher on matrix multiplication you can go here. First we are going to start with a very basic matrix multiplication algorithm that you can find in about a million places on the interwebs.
for (int i = 0; i < resultMatrixHeight; i++)
{
for (int j = 0; j < resultMatrixWidth; j++)
{
for (int k = 0; k < matrix1Width; k++)
{
result1[i, j] += matrix1[i, k] * matrix2[k, j];
}
}
}
In this algorithm we are merely going through the result matrix row by row and then we loop through our two other matrices and add up the cooresponding products for the particular cell of the result matrix that we are on. I wanted to use it since it is a pretty simple algorithm and it is O(n3) so it will take a while to run for large input matrices. This will allow us to see big performance gains when we start to write our super awesome parallel algorithms. I don’t know about you, but I’m feeling smarter already.
To run my tests I have created two matrices, one is 2000 x 2000 square and the other is 3400 x 2000. I decided to use very large matrices so that I could get a better idea of the performance difference in my parallel algorithms. I am also populating these matrices with random integers between 1 and 20. I am running these tests on a machine with these specs:

How bad is it when you are so lazy that you take a screenshot of your system specs rather than type them in? So, you can see I am on a dual-core CPU so we can get some decent parallel numbers, but not like we would if I had a quad core box. If anyone wants to send me one, please feel free.
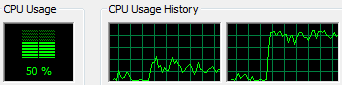
During the single threaded run my system saw the expected 50% load (note that all performance pics were taken during different runs than the results I am posting because the taskmanager affects the results):
Our results for the single threaded run looked like this:
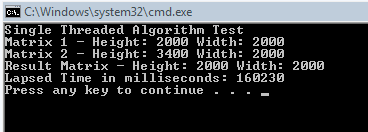
So it took about 160 seconds to process the 4 million entries in the result matrix. Pretty fast, we clearly don’t need to parallelize this, it is already fast. So, hope you enjoyed the post!
Ha, I wish. Before we start looking at my first stab at a parallel algorithm, lets look first at the Parallel.For statement. The signature for this method that we are going to use looks like this (this is the most basic overload of this method):
public static void For(int fromInclusive,
int toExclusive, Action<int> body);
The first parameter is the integer you are starting from, in our case this is 0. The second parameter is the last number we are going to, but this number is exclusive. So, if we pass 0 and 100 then we are going to iterate from 0 to 99. Next the method takes an Action<int> delegate. An Action<int> delegate returns void and takes an integer as its single parameter. So, it just passes in the current index that you are operating on.
So, my first stab at parallizing this using the Parallel.For statement looked like this:
Parallel.For(0, resultHeight,
i =>
{
for (int j = 0; j < resultWidth; j++)
{
for (int k = 0; k < matrix1Width; k++)
{
Interlocked.Add(ref result2[i, j],
matrix1[i, k] * matrix2[k, j]);
}
}
}
);
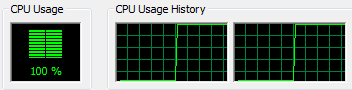
Initially I thought that this might be a *bit* faster than the single threaded algorithm, but the overhead involved with the Interlocked.Add was just too much. During the execution of the run my CPU did spike to 100%:
But the overhead was just too much and our results ended up looking like this:
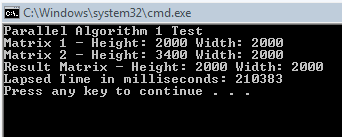
It took over 210 seconds now to process the same size matrices! Well, that does not provide us with promising results, but it is *possible* that if we had a quad core box that we could overcome the cost of Interlocked.Add and still process these matrices faster. The good news is though that we don’t need four cores, we can find a better way to do this.
I looked at our previous parallel algorithm and though "how can we get rid of the call to Interlocked.Add". Well, the answer is to use ThreadLocalState. This is another feature of Parallel.For method. You can tell it a type that you are going to use to maintain state within a single thread (not for each iteration) in our method. The overload that we are going to use looks like this:
public static void For<TLocal>(int fromInclusive,
int toExclusive, Func<TLocal> threadLocalSelector,
Action<int, ParallelState<TLocal>> body);
A wee bit more complicated that our last Parallel.For overload and it needs a bit of explanation. First there is a parallel parameter "TLocal" that we can pass to tell the method what type our ThreadLocalState is going to be. I’ll explain this in a second. The first two parameters operate exactly the same as they did previously, but the next parameter is a Func delegate that returns the same type as our ThreadLocalState. It is named threadLocalSelector and is used to initialize our thread state. In our case the type is "int" and so we are just returning 0. The next parameter is another Action delegate like we used before, only this time there are two parameters. One is our indexer and the other is the ThreadLocalState.
So, I decided to go ahead and use this ThreadLocalState in my algorithm in order to accumulate the results. My implementation looks like this:
Parallel.For<int>(0, resultHeight,
() => 0,
(i, state) =>
{
for (int j = 0; j < resultWidth; j++)
{
state.ThreadLocalState = 0;
for (int k = 0; k < matrix1Width; k++)
{
state.ThreadLocalState += matrix1[i, k] * matrix2[k, j];
}
Interlocked.Add(ref result3[i, j], state.ThreadLocalState);
}
}
);
So, between each time we change the position in our result array we zero out our thread state and then we loop through and do our calculations adding the results to our local state, thereby avoiding having to use Interlocked.Add until we get to the end of our calculations. Then we call Interlocked.Add and add our accumulated value to the appropriate place in our result array. The results end up looking like this:
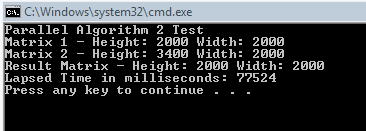
Now that is a bit more like it. Quite a bit faster than our original single threaded algorithm. After I saw this I patted myself on the back and began to move on, until I realized that I was an idiot.
Realization 1: notice how my multi-threaded algorithm actually takes less than half of the time to run than my original single threaded algorithm. How is this?
Realization 2: This whole time I had my head stuck in the "Parallel programming lock everything" mindset that I failed to realize that my algorithm didn’t require any locking! I noticed that we aren’t modifying matrix1 or matrix2 at all, so obviously they don’t require locking. But since we are dividing up our threading on the "i" indexer you will notice that this means that no two threads will ever modify the same index in our result array since they will always have different values of "i"!
Realization 1 made me understand that in my ThreadLocalState implementation, a lot of the speedup of the algorithm was due to the fact that we weren’t adding directly to the array in every loop. This was causing us to do a large number of array lookups, so moving to the ThreadLocalState sped us up in this area as well, and gave us an even bigger speed boost.
Realization number 2 made me feel a bit sheepish. After I noticed that I really didn’t need to have locking, I decided that a rewrite of the algorithm was in order.
So, with this under my belt, I produced this:
Parallel.For(0, resultHeight,
i =>
{
for (int j = 0; j < resultWidth; j++)
{
int sum = 0;
for (int k = 0; k < matrix1Width; k++)
{
sum += matrix1[i, k] * matrix2[k, j];
}
result3[i, j] = sum;
}
}
);
Now look how simple that is. And unless I am totally missing something (which is quite possible), there is no locking needed. So, running our newest algorithm, we get this result:
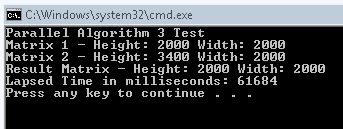
There you have it, we shaved over 15 seconds off our last time. And almost exactly half of the time we got after I rewrote the single threaded algorithm to use a local sum variable (The rewritten single threaded method took 121 seconds). So, I hope you enjoyed my little foray through the Parallel.For method and hopefully your adventure with ParallelFX won’t waste quite as much time as mine did. 🙂 Also, I’m sure that someone is going to point out how this algorithm can be faster, so I am going to go ahead and ask for suggestions on how to make it faster. Anyone have any ideas?
Loved the article? Hated it? Didn’t even read it?
We’d love to hear from you.




I did a similar thing and posted the core loops.
http://www.e128.info/search/label/performance
@Brent: Cool, I’ll definitely have to check it out.
I’m very curious as to what the overhead is on this. The benifit is clear on big loops. But what if you have many small, ie in a web application scenario?
For example a small loop of 10-100 items executed on each request. Would there be a benifit in using ParallelFX or the startup overhead would diminish any potential gain?
Well, I had to use big loops in order to make it worthwhile. The overhead of spawning multiple threads is huge in situations like this. For small loops, even up to a few hundred thousand items you probably won’t see much gain when you are doing something as fast as integer calculations. But it is all in how long your operations take. I am working on a post now involving string sorting with ParallelFX and so far I am seeing gains in much smaller sets of data.
May I also suggest some regex matching tests? I think that’s a pretty common pattern as well, just dont use a trivial expression.
you can use temporal locality with sub-matrix multiplication
for it := 1 to n by s do
for kt := 1 to n by s do
for jt := 1 to n by s do
for i = it to min(it+s-1, n) do
for k = kt to min(kt+s-1, n) do
for j = jt to min(jt+s-1, n) do
c[i,j] = c[i,j] + a[i,k] � b[k,j]
endfor
endfor
endfor
endfor
endfor
endfor
notice that loop order is now ikj instead of i j k because
fetching matrix2[k, j]; is slow because it dont use caching (matrix are stored row major)
How did you come up with a result matrix of size 2000×2000 by multiplying matrices in sizes 3400×2000 and 2000×2000 ? From wikipedia:
[quote]If A is an m-by-n matrix and B is an n-by-p matrix, then their product is an m-by-p matrix[/quote]
In your case m=3400, n=2000 and p=2000 which must result to a matrix with the size 3400×2000. Am I missing something?