In my previous post I talked about Linq expression trees and how you can create them in several ways. We talked about how you could create them simply using a lambda expression:

Expression<Func<int, int>> lammy = n => n * 2;

Or how you could create them manually:

ParameterExpression param = Expression.Parameter(typeof (int), "n");

BinaryExpression body = 

    Expression.Multiply(param, Expression.Constant(2, typeof (int)));

lammy = Expression.Lambda<Func<int, int>>(body, param);

I then showed you some code that would allow us to parse out a string of numbers and math operations and build up an expression tree. Everything looked great, all we had to do was keep parsing our string and chaining the Expressions together using our GetMathExpression method:

public Expression GetMathExpression(char operation, 

            Expression leftExpression, Expression rightExpression)

        {

            switch (operation)

            {

                case '*':

                    return Expression.MultiplyChecked(leftExpression, rightExpression);

                case '+':

                    return Expression.AddChecked(leftExpression, rightExpression);

                case '/':

                    return Expression.Divide(leftExpression, rightExpression);

                case '-':

                    return Expression.SubtractChecked(leftExpression, rightExpression);

            }

            return null;

        }

So, we just parse through our math operation building up our expression tree. But, as we discussed in the last post, there is a problem. The tree that we built up is going to be in the order that we had in the math equation that we entered. It is totally ignoring order of operations and just going sequentially down the string. So, for a string of “5+2*5+3” we would end up with a tree that looks like this:

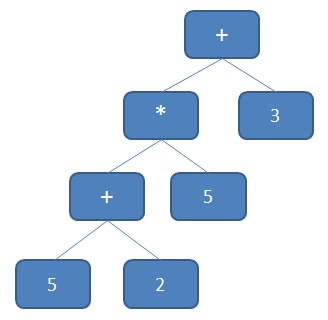
Which ends up producing an incorrect answer to our equation, since it would be evaluated as: ((5 + 2) * 5) + 3.

So, what would we have to do in order to get this to evaluate correctly? Well, we would have to manipulate this tree until it took the form of 5 + (2 * 5) + 3. This would create a tree that looks like this:

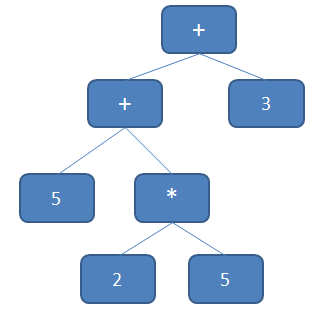
This way, the 2 * 5 would get evaluated instead of 5 + 2. So you will see that the logic we are employing is simply to start from the top of the tree and start walking down the tree looking for nodes where the order of operations of the child is less then the parent. This is true when we hit the multiply node in the first tree (since add has a lower order of operation than the parent). So, we need to move the + sign up and move the multiplication down.

The steps that you will follow in order to do this is:

1. Move the + node in place of the * node, effectively removing the * nodes left node
2. Remove the + node’s right child and replace it with the * node
3. Set the + node’s former right child as the left node of the * node

This will move the add above the multiply which will cause it to be evaluated later. So, how do we do this in code?

Well, the first thing we have to do is to be able to walk our expression tree. In this example we are using almost all binary expressions, so it probably wouldn’t be too hard to walk this tree, but not all linq expressions have two children. Some have more properties and expressions to them, and it would require quite a bit of code to walk all the different types of expressions. Luckily Microsoft has helped us out with this. In this MSDN page Microsoft shows you how to create an expression visitor, which is just a class that has knowledge of how to walk an expression tree. All of the methods to handle each type of expression are virtual, so you can plug your own logic in as you walk the tree.

Whatever gets returned from each of these methods is used to build up the resulting tree. In this way, by changing what is returned from these methods, we can manipulate the tree. So, first I am going to create a class called OrderOfOperationsVisitor that descends from the ExpressionVisitor class that I pulled from Microsoft.

public class OrderOfOperationsVisitor : ExpressionVisitor

Okay, so we have our class signature and now we just need to overload our method:

protected override Expression VisitBinary(BinaryExpression b)

{

    if ((b.Left is BinaryExpression) && IsChildOrderOfOperationsLower(b, b.Left))

    {

        this.SwapOccurred = true;

        return SwapLeft(b, (BinaryExpression)b.Left);

    }

    if ((b.Right is BinaryExpression) && IsChildOrderOfOperationsLower(b, b.Right))

    {

        this.SwapOccurred = true;

        return SwapRight(b, (BinaryExpression) b.Right);

    }

    return base.VisitBinary(b);

}

Okay, so this where the magic begins. You can see that we are looking at the children of our BinaryExpression and then testing it to see the order of operations is lower. If it is, then we set a property on our class called “SwapOccurred” to true (remember this for later) and then we swap the current node with that child. If neither node is swapped, then we simply continue on down our tree by calling base.VisitBinary(b) which will simply walk the children of this node.

Since we are only supporting +, -, /, and * our “IsChildOrderOfOperationsLower” method will look like this:

private bool IsChildOrderOfOperationsLower(Expression current, Expression child)

{

    if (current.NodeType == ExpressionType.MultiplyChecked 

        || current.NodeType == ExpressionType.Divide)

    {

        if (child.NodeType == ExpressionType.AddChecked ||

            child.NodeType == ExpressionType.SubtractChecked)

        {

            return true;

        }                

    }            

    return false;

}

And our swap methods look like this:

private Expression SwapLeft(BinaryExpression expression, BinaryExpression left)

{

    Expression right = Expression.MakeBinary(expression.NodeType, left.Right, expression.Right);

    return Expression.MakeBinary(left.NodeType, left.Left, right);            

}

private Expression SwapRight(BinaryExpression expression, BinaryExpression right)

{

    Expression left = Expression.MakeBinary(expression.NodeType, expression.Left, right.Left);

    return Expression.MakeBinary(right.NodeType, left, right.Right);

}

Easy enough to see what is happening there. I am creating new expressions to do exactly the process that we outlined above for swapping a node with its parent.

Now we just have to use this class on our newly constructed tree:

var orderOfOperationsVisitor = new OrderOfOperationsVisitor();

mathExpression = orderOfOperationsVisitor.Visit(mathExpression);

while (orderOfOperationsVisitor.SwapOccurred)

{

    orderOfOperationsVisitor = new OrderOfOperationsVisitor();

    mathExpression = orderOfOperationsVisitor.Visit(mathExpression);

}

Notice that we run it once, then we start looping on “SwapOccurred”. This is because after we reorder the nodes, we simply return the nodes back from our method and stop walking the tree there. We need to check below that node in the tree to make sure that there isn’t anything below it that needs to be swapped. Another issue is that a node may need to be moved up multiple levels. Like this:

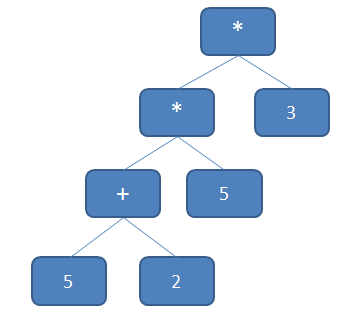
Since we can’t walk the tree backwards, we have to make multiple passes in order to get the ‘+’ node to the top.

So, now that we have done all of this, we can look at our expression tree before:

and after:

Success!

Well, I hope that you have found this little two part series on expression trees to be useful. I have attached the source for this project here, so feel free to download it and play around with it!