
In my last post I introduced you to the new HashSet class in .net 3.5. I showed you how easy it was to do a plethora of set operations using this class. Well, Dave over at Encosia saw this class and thought it might be a good fit for a program he had wrote that searched through variable length letter permutations to find items in a list of valid strings. He wondered if it might be faster to load up a HashSet and do an intersect operation than the current method he had of using the Dictionary class to lookup valid words. So, I asked him to send me over the source so that I could do a bit of performance testing. He happily sent me the source, and so here is my performance comparison between the two.
Method 1: This method uses a Dictionary. It first opens up the word file and loads up the Dictionary with the words. It then takes the input string and generates all the permutations of it. After each permutation is generated it checks the Dictionary of valid words using the "ContainsKey" method.
Method 2: This method uses a HashSet. It starts off like Method 1 and opens the word file and loads the HashSet with the valid words. It then generates all of the permutations and loads them into a second HashSet. It then calls the "IntersectWith" method on the first HashSet passing in the second HashSet which returns the valid words.
The tests were run in a loop of 10 passes with 500 lookups per pass. Lets look at the results and then discuss:
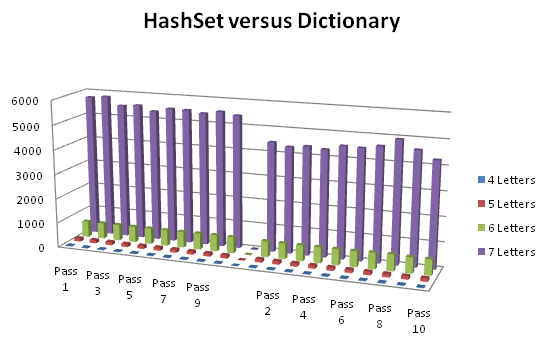
As you can see, in the 4, 5, and 6 letter combinations the numbers look very similar. For 6 letters it took roughly 650 milliseconds to do 500 looks-ups. When we hit the 7 letter mark things start looking very different. The Dictionary begins to pull ahead by a good margin. The HashSet had an average time of 5529 milliseconds and the Dictionary averaged 4495 milliseconds. A different of more than 20%! So, why the sudden difference? Well, the HashSet method goes through all of the possible permutations and loads up a giant HashSet object with all of those permutations. So, at 6 letters we have 1956 possible permutations, but since it jumps up to 13700 permutations at 7 letters, it begins to seriously affect the performance of the HashSet method.
Now, at this point you may be saying "Heyyyyy! 6 letters only has 6! (720) possible combinations!" And you would be partially correct, but we are doing all combinations including lengths of 5,4,3,2, and 1. The formula for calculating this is:
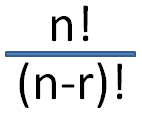
In this forumla n is the set size and r is the size of the permutation. So 6 letters is actually 6!/(6-6)! + 6!/(6-5)! + 6!/(6-4)! etc…
So, looking at this you might think that the choice between Dictionary and HashSet is easy if you are dealing with large sets, and you’d be wrong. 🙂 The issue is that the HashSet spent most of its time loading up the second HashSet in order to do the "Intersection" operation. Well, the HashSet also has a "Contains" method so we really didn’t need to load up the second HashSet at all! If we switch out the HashSet in the Dictionary method and replace "ContainsKey" with the "Contains" method we end up with almost identical performance even at 7 characters.
So, in the end, these two classes have almost identical lookup speeds, the real question is whether you need the ability to assign a key to a piece of data (the dictionary has a seperate key and value type, the HashSet does not) or whether you need the robust set operations that are given to you by the HashSet object.
And finally, if you want to see the code that was generating the permutations for the HashSet and the Dictionary, here it is:
//HashSet Permutations
public void GeneratePermutations(HashSet<string> permutations,
string prefix, List<char> letters)
{
for (int i = 0; i < letters.Count; i++)
{
_permutations++;
string word = prefix + letters[i];
List<char> j = new List<char>(letters);
permutations.Add(word);
j.RemoveAt(i);
GeneratePermutations(permutations, word, j);
}
}
//Dictionary Permutations
protected void GeneratePermutations(List<string> results,
string prefix, List<char> letters)
{
for (int i = 0; i < letters.Count; i++)
{
_permutations++;
string word = prefix + letters[i];
List<char> j = new List<char>(letters);
if (CheckWord(word))
results.Add(word);
j.RemoveAt(i);
WordSearch(results, word, j);
}
}
Loved the article? Hated it? Didn’t even read it?
We’d love to hear from you.



[quote]So, in the end, these two classes have almost identical lookup speeds, the real question is whether you need the ability to assign a key to a piece of data (the dictionary has a seperate key and value type, the HashSet does not) or whether you need the robust set operations that are given to you by the HashSet object.[/quote]
Oddly enough, I only use the Dictionary because List<string>.Contains() and SortedList<string>.BinarySearch() ran much slower than Dictionary<string, int>.ContainsKey(). I don’t actually store any data in the Dictionary’s value, other than a 0 to make it happy.
I didn’t have time to dig into what was going on with that, but the difference was very noticeable.
I may give it a try with HashSet.Contains() soon and see if it performs better.
Interesting comparison. Thanks for the good info!
What about memory usage? I would guess it is pretty close.
I like benchmarks like this, even though this particularly one won’t do much but answer a little question in my mind.
Sorry, I did not get a chance to profile the memory usage on these two classes. Maybe that’ll be something for a future post. My bet would be that the HashSet would be lighter on the memory since both the Dictionary and HashSet store their data in a very lightweight struct, but the Dictionary has a key and a value, whereas the HashSet only stores a value.