
This Thursday we (as in the Richmond VA community) are having a Meet and Code dinner where we are going to be talking about Linq Expression trees. A while back I made a post about dynamically generating Lambdas, and since the topic of the dinner this Thursday is Expression trees, I wanted to throw together a demo that uses dynamically constructed expression trees to do something useful. So, if you are attending this Thursday, then you may want to skip this post so that you’ll have something new to see this Thursday!
In case you don’t know what Linq Expression Trees are, they are ASTs (Abstract Syntax Trees) that can be built out of lambdas or Linq expressions. If you want to get an expression tree out of a lambda then you can simply wrap the Func delegate in the generic Expression class like this:
Expression<Func<int, int>> lammy = n => n * 2;
Interesting isn’t it? Yep, the C# compiler actually generates two different things based on the type you are assigning to! (Did you know that MSIL supports overloading by return type?) So, if I were to do this, it would generate the actual delegate:
Func<int, int> lammy = n => n * 2;
Kinda cool, but that isn’t what we are talking about here. What we are here for is to learn how these suckers work. So, what does the expression tree from the above Expression look like?
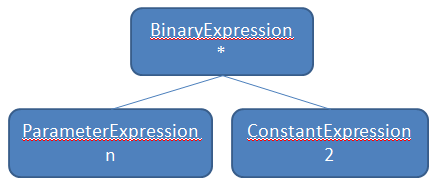
Now you can see why it is called an abstract syntax tree. I removed the Lambda expression that this is wrapped in, but this is the important part. Here you see that we have a BinaryExpression of type Multiply (or CheckedMultiply) with a left and right node that represent the parameter to the lambda and the constant value of two.
Now, these syntax trees come in handy for a variety of reasons (there are probably a few more):
- Tree modification before execution – You can actually modify the tree before it is compiled. You could join operations or simplify the tree before compiling it.
- Combining trees: This is in line with number 1, but you can take multiple expression trees and combine them using new Expression tree nodes. (Yes, you can manually generate these, and we will get into those later on)
- Alternate Execution: You can take an expression tree and interpret it and execute it in your own manner. This is precisely what Linq To Sql does. It takes an expression tree and interprets it, then turns it into SQL instead of runnable MSIL.
So, in this post I am going to look at 1 and 2. But first lets look at how we would build up an expression tree manually. In order to build the above expression manually the code would look like this:
ParameterExpression param = Expression.Parameter(typeof (int), "n");
BinaryExpression body =
Expression.Multiply(param, Expression.Constant(2, typeof (int)));
lammy = Expression.Lambda<Func<int, int>>(body, param);
Not too hard to follow. We declare our parameter and then we declare our lambda body as an multiply BinaryExpression with the left op being the param and the right op being the constant value 2. We can then create our lambda expression passing in our body and our parameters. In order to use this lambda, all we have to do is call:
Func<int,int> delly = lammy.Compile();
And now we have a usable delegate that we can call. Pretty sweet, but you are probably thinking, why would I want to go through all that when I can just say:
Func<int, int> delly = n => n * 2;
And you’d be right, if you already knew what the lambda was going to be. But what if you don’t know what the lambda is going to be? Then how would you define it in that nice little syntax. Well, you wouldn’t, you’d have to build it up yourself. But the good news is that it is very possible.
So, lets say that you are building a calculator program. Wow, I just happened to have built one as an example! That is amazing! And so I want to be able to enter a string of math operations like this:
5+2*5+3
Well, we could walk from left to right taking each number and math operation building up a tree as we go. The result would end up looking something like this:
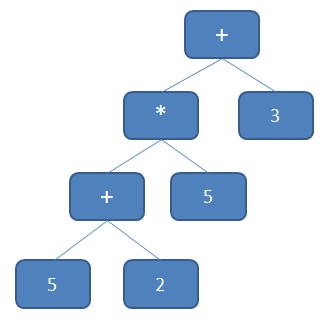
If you have ever had to do much tree traversal, you will notice that this tree will most likely be evaluated using a depth first in-order traversal. So what will happen is that we start at the top with the ‘+’ and we will go to the left child, and then when we get there we will go to its left child until we run out of left children. So, we will hit the 5 and then pop back up to the ‘+’ and then we will go for the right child which is ‘2’. So, 5 + 2 is evaluated to 7 and then 7 * 5 is evaluated to 35 and then we add 35 + 3 to get 38. We just keep falling back up the tree going left, center, right. The code used to get here looks something like this (several method calls are factored out, but they have meaningful names):
string currentDigit = string.Empty;
char currentOperation = ' ';
foreach (char c in equation)
{
if (Char.IsDigit(c))
{
currentDigit += c;
}
else
{
if (!String.IsNullOrEmpty(currentDigit))
{
if (leftExpression == null)
{
leftExpression = GetDigitConstant(currentDigit);
}
else
{
rightExpression = GetDigitConstant(currentDigit);
mathExpression =
GetMathExpression(currentOperation, leftExpression, rightExpression);
leftExpression = mathExpression;
}
currentDigit = string.Empty;
}
currentOperation = c;
}
}
rightExpression = GetDigitConstant(currentDigit);
mathExpression = GetMathExpression(currentOperation, leftExpression, rightExpression);
Func<int> func = CompileExpression(mathExpression);
The only problem with this is that it is wrooooooooooooooong (and it is pretty ugly)! Ever heard of a little thing called order of operations?
If, by some small miracle, you have not heard of order of operations I am going to simplify it for you real quick. Since my app doesn’t support parenthesis, and only basic math functions such as *, /, +, – we are just going to say that you do all * and / before + and -. So, if you had 5+3*6 the answer would be 23 and not 48.
If we wanted to get our math expression into order of operations, how would we do it? Would we do several passes through our expression string and try to build up our multiplies and divides first and then do some fancy stuff in order to get it all in order? Or could we just build our tree and then manipulate it in tree form? Hmmmmmmm. Well, when dealing with trees there are tons well known manipulations you can do in order to the tree in the form you want, so I think I am going to go that route….
Sorry, it is getting pretty late, I think I am going to stop there for the evening. In the next installment I am going to talk about the expression visitor class and how we can use it to correct our order of operations problem. I will also attach the source code to the entire project in the next post. I hope this helps!
Loved the article? Hated it? Didn’t even read it?
We’d love to hear from you.




